| Video | 🕸 |
| Paper | 🕸 |
| Code | 🕸 |
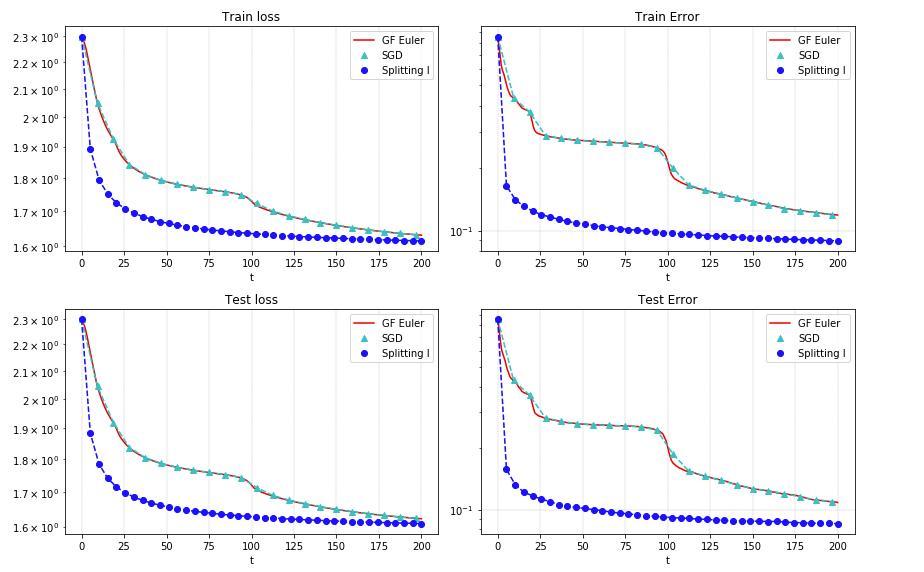
We present a different view on stochastic optimization, which goes back to the splitting schemes for approximate solutions of ODE. In this work, we provide a connection between stochastic gradient descent approach and first-order splitting scheme for ODE. We consider the special case of splitting, which is inspired by machine learning applications and derive a new upper bound on the global splitting error for it. We present, that the Kaczmarz method is the limit case of the splitting scheme for the unit batch SGD for linear least squares problem. We support our findings with systematic empirical studies, which demonstrates, that a more accurate solution of local problems leads to the stepsize robustness and provides better convergence in time and iterations on the softmax regression problem.