| Paper | 🕸 |
| Code | 🕸 |
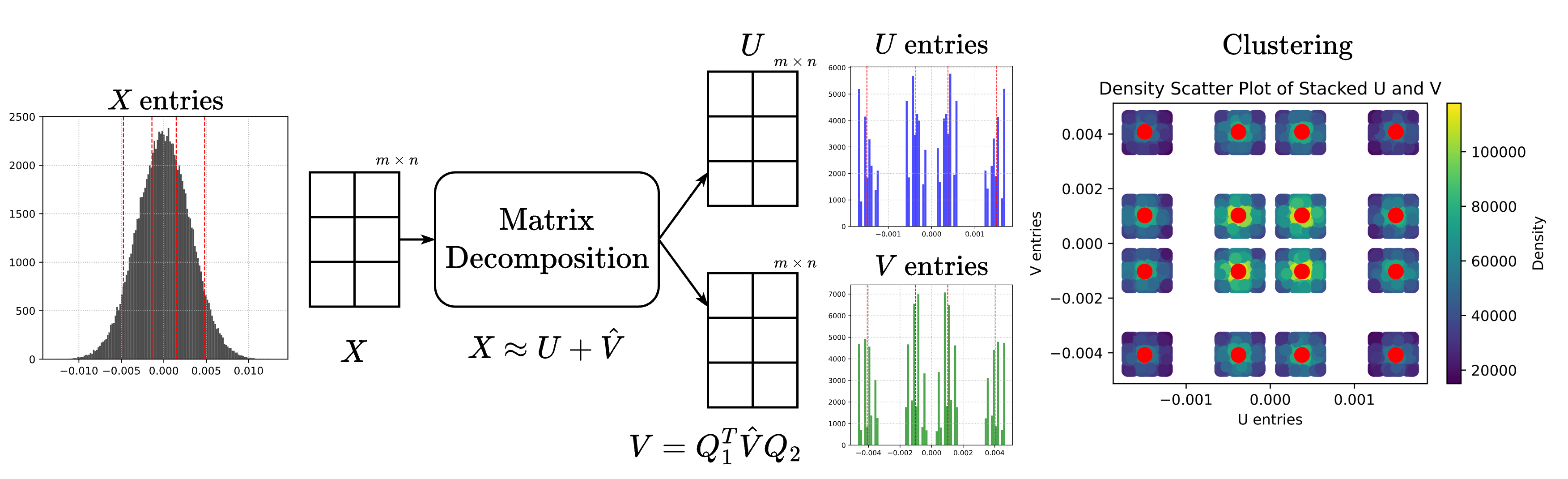
In this paper, we introduce an algorithm for data quantization based on the principles of Kashin representation. This approach hinges on decomposing any given vector, matrix, or tensor into two factors. The first factor maintains a small infinity norm, while the second exhibits a similarly constrained norm when multiplied by an orthogonal matrix. Surprisingly, the entries of factors after decomposition are well-concentrated around several peaks, which allows us to efficiently replace them with corresponding centroids for quantization purposes. We study the theoretical properties of the proposed approach and rigorously evaluate our compression algorithm in the context of next-word prediction tasks, employing models like OPT of varying sizes. Our findings demonstrate that Kashin Quantization achieves competitive quality in model performance while ensuring superior data compression, marking a significant advancement in the field of data quantization.