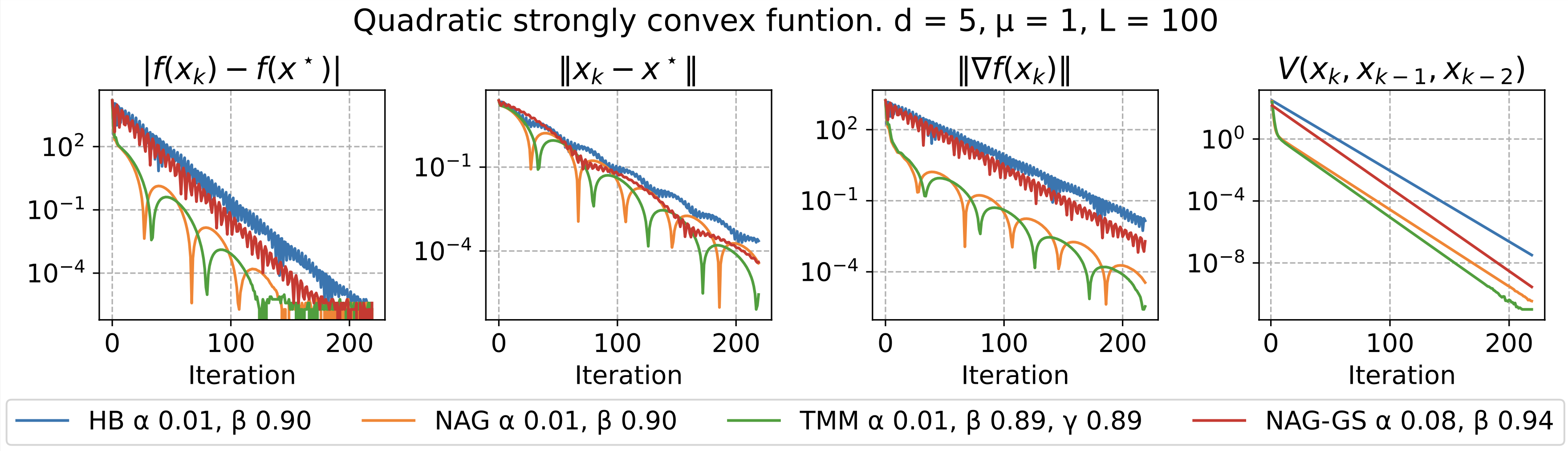
Lyapunov functions play a fundamental role in analyzing the stability and convergence properties of optimization methods. In this paper, we propose a novel and straightforward approach for constructing Lyapunov functions for first-order methods applied to quadratic functions. Our approach involves bringing the iteration matrix to an upper triangular form using Schur decomposition, then examining the value of the last coordinate of the state vector. This value is multiplied by a magnitude smaller than one at each iteration. Consequently, this value should decrease at each iteration, provided that the method converges. We rigorously prove the suitability of this Lyapunov function for all first-order methods and derive the necessary conditions for the proposed function to decrease monotonically. Experiments conducted with general convex functions are also presented, alongside a study on the limitations of the proposed approach.

Remarkably, the newly discovered Lyapunov function is straightforward and does not explicitly depend on the exact method formulation or function characteristics like strong convexity or smoothness constants. In essence, a single expression serves as a Lyapunov function for several methods, including Heavy Ball, Nesterov Accelerated Gradient, and Triple Momentum, among others. To the best of our knowledge, this approach has not been previously reported in the literature.